มุฮัมมัด อิบนุ มูซา อัลคอวาริซมีย์ (เสียชีวิตประมาณ ปี ค.ศ. 850) หนึ่งในนักปราชญ์ที่ทำงานในหอสมุดบัยตุลฮิกมะห์ และหอสังเกตการณ์ทางดาราศาสตร์ในมหานครแบกแดด ตลอดสมัยของเคาะลีฟะห์อัลมะมูน (ปกครองช่วงปี ค.ศ. 813-833)
จากชื่อของท่านแสดงว่าเป็นคนที่มีพื้นเพมาจากภูมิภาคคอวาริซม์ ทางตอนใต้ของทะเลสาบอะราลในเอเซียกลาง ประทศอุสเบกิซสถานปัจจุบัน เป็นทั้งนักดาราศาสตร์ ภูมิศาสตร์และคณิตศาสตร์
งานเขียนทางด้านดาราศาสตร์ของเขาประกอบด้วยตำรา Zij Al Sind wal Hind (ตารางข้อมูลทางดาราศาสตร์ของอินเดีย) มี 37 บท ประกอบด้วยข้อมูล 116 ตาราง เกี่ยวกับปฏิทิน ข้อมูลตำแหน่งการโคจรของดวงอาทิตย์ ดวงจันทร์และดาวเคราะห์ทั้ง 5 ข้อมูลการทำนายตามโหราศาสตร์ของอินเดีย และสุดท้ายคือตารางค่า Sine ต้นฉบับของหนังสือเล่มนี้สูญหายไปแล้ว แต่มีฉบับปรับปรุงที่เขียนโดยนักดาราศาสตร์อันดะลุส (สเปนสมัยอยู่ใต้ปกครองของมุสลิม) ชื่อมัสละมะห์ อิบนุ อะหมัด อัลมัจรีฏีย์ (เสียชีวิต ค.ศ. 1010 เป็นชาวเมืองมัจรีฏหรือแมดริดในปัจจุบัน) ซึ่งต่อมาถูกแปลเป็นภาษาละตินครั้งแรกโดยอดิลาร์ดแห่งบาธ (มีชีวิต ค.ศ. 1116 – 1142) อัลคอวาริซมีย์ยังเขียนตำราการคำนวณปฏิทินแบบฮิบรู Risala fi Istikhraj Tarikh Al Yahud และเป็นผู้ออกแบบแอสโตรแล็บและนาฬิกาแดดที่มีความเที่ยงตรงสามารถประยุกต์ใช้กับภูมิภาคต่างๆ ทำให้นาฬิกาแดดกลายเป็นอุปกรณ์ที่แพร่หลายสำหรับมัสยิดในการกำหนดเวลาละหมาด
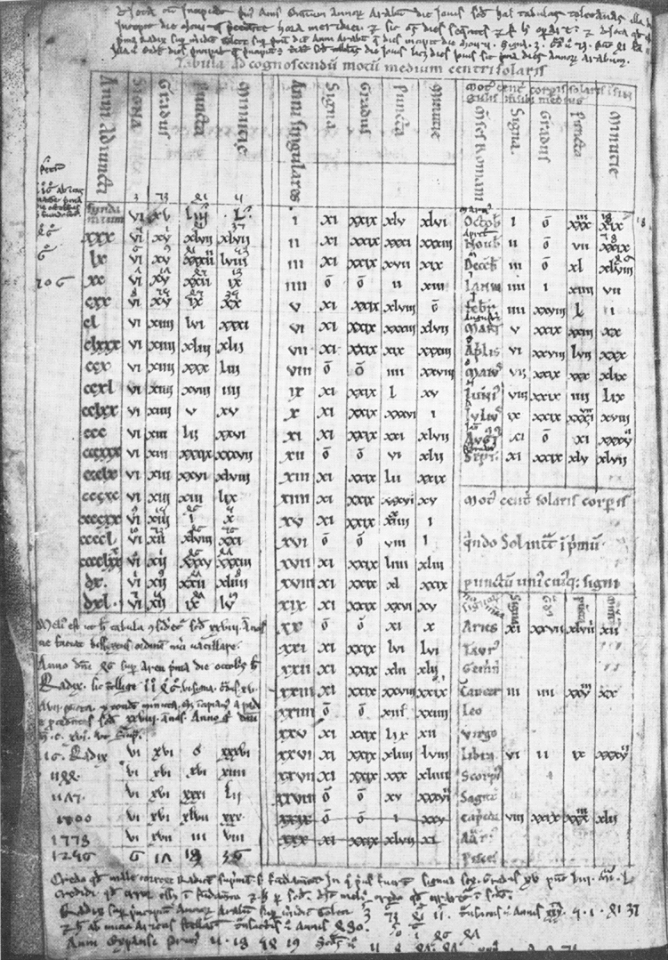
รูปที่ 1 ตารางข้อมูลทางดาราศาสตร์ จากหนังสือ Zij ฉบับที่แปลเป็นภาษาละติน

รูปที่ 2 ส่วนหนึ่งของตำรา al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wal-muqābala
ผลงานทางภูมิศาสตร์ได้แก่ Kitāb Ṣūrat al-Arḍ ( كتاب صورة الأرض, "Book of the Description of the Earth") เป็นการปรับปรุงแผนที่โลกของทอเลมี ระบุตำแหน่งเป็นค่าลองติจูดและละติจูดของเมือง ภูเขา แม่น้ำ ทะเล เกาะและสถานที่สำคัญๆถึง 2,440 แห่ง ขณะนี้ มีต้นฉบับภาษาอาหรับเฉพาะหนังสือ (โดยแผนที่ประกอบหายไป)เหลืออยู่เพียงเล่มเดียว ที่หอสมุด Strasbourg University ประเทศฝรั่งเศส ส่วนฉบับแปลเป็นภาษาละตินเหลืออยู่ที่ Biblioteca Nacional de España ประเทศสเปน
อัลคอวาริซมีย์ไม่ได้มีความโดดเด่นในฐานะนักดาราศาสตร์ หากแต่เป็นนักคณิตศาสตร์ ผู้วางรากฐานพีชคณิต จนได้รับการยอมรับว่าเป็น “บิดาแห่งพีชคณิต” และ “นักคณิตศาสตร์ผู้ยิ่งใหญ่แห่งอาหรับ” ตำราที่มีชื่อเสียงของท่านคือ الكتاب المختصر في حساب الجبر والمقابلة al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wal-muqābala
“อัลจับรุ” al-jabr แปลว่าการนำส่วนที่ขาดหายไปคืนกลับมา (Restoring) เพื่อทำให้ค่าทั้งสองข้างของสมการเท่ากัน ส่วนคำว่า “อัลมุกอบะละห์” al-muqābala แปลว่าการสร้างขึ้นเป็นสมการ ซึ่งทั้งสองข้างของสมการมีค่าเท่ากัน หนังสือเล่มนี้เป็นการประยุกต์ทางพีชคณิต แก้สมการเพื่อหาค่าตัวแปรโดยใช้คุณสมบัติการบวก ลบ คูณ หาร ตลอดจนการเปรียบเทียบ เท่ากัน มากกว่า/น้อยกว่า มีเลขศูนย์ เลขทศนิยม เศษส่วน เลขยกกำลังและรากมาเกี่ยวข้อง แสดงการคิดโจทย์ตัวอย่างมากกว่า 800 ข้อ บางส่วนก็เป็นข้อที่กลุ่มนีโอบาบิโลเนียนเคยขบคิดมาก่อนแล้ว
สมการทั้งหมดของอัลคอวาริซมีย์เป็นสมการเชิงเส้นและสมการกำลังสอง เขาเสนอวิธีการลดรูปของสมการให้เหลือเป็นหนึ่งใน 6 สมการมาตรฐานที่เขาได้จำแนกไว้ (รูปที่ 5 ) สมการของเขายังไม่ได้ใช้สัญลักษณ์ใดๆ หากแต่ใช้ประโยคอธิบายโจทย์ปัญหา แล้วใช้แผนผัง/แผนภาพแสดงการแก้โจทย์ (ดูตัวอย่างการแก้สมการของอัลคอวาริซมีย์โดยใช้เทคนิคทางเรขาคณิต ในรูปที่ 6 ) เขากล่าวถึงตัวแปรที่ไม่ทราบค่าของสมการเหล่านั้นว่า شيء ( Shay’ ชัยอฺ) แปลว่าอะไรบางอย่างที่เราไม่รู้ ตอนที่คริสเตียนยึดสเปนคืนจากมุสลิมในคริสตวรรษที่ 12 ก็ได้แปลตำราเล่มนี้เป็นภาษาละติน แต่มีปัญหาในการแปล เนื่องจากภาษาสเปนไม่มีเสียง ช. ชาวสเปนออกเสียงคำว่า “ชัยอฺ” ไม่ถนัดนัก จึงเขียนทับศัพท์คำนี้ว่า Xei ซึ่งต่อมาเหลือเพียงตัว X ที่เรามักใช้แทนตัวแปรในสมการทางคณิตศาสตร์จนถึงปัจจุบัน

รูปที่ 3 ที่มาของการใช้ x แทนสิ่งที่เราไม่รู้
ที่มา https://www.facebook.com/
ที่มา https://www.facebook.com/
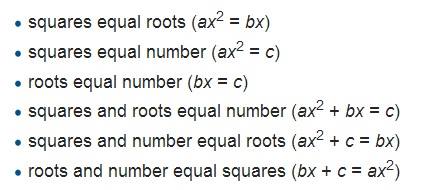
รูปที่ 4 สมการมาตรฐาน 6 รูปแบบพร้อมตัวอย่าง ที่อัลคอวาริซมีย์ได้จำแนกไ
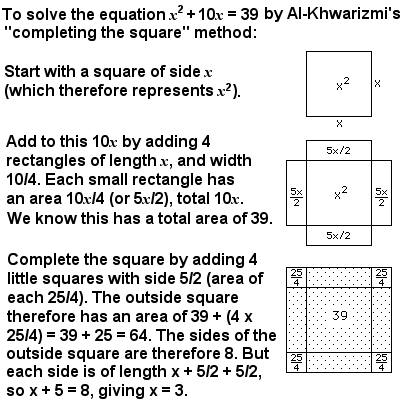
รูปที่ 5 ตัวอย่างการแก้สมการของอัลค
1. ยกกำลังค่า x จะได้พื้นที่สี่เหลี่ยมจตุร
2. เพิ่มค่า 10x โดยเป็นพื้นที่สี่เหลี่ยมผื
3. เพิ่มพื้นที่ 4 เหลี่ยมจตุรัสขนาดเล็กที่มุ
4. สี่เหลี่ยมจตุรัสใหญ่ที่มีค
1. ยกกำลังค่า x จะได้พื้นที่สี่เหลี่ยมจตุร
2. เพิ่มค่า 10x โดยเป็นพื้นที่สี่เหลี่ยมผื
3. เพิ่มพื้นที่ 4 เหลี่ยมจตุรัสขนาดเล็กที่มุ
4. สี่เหลี่ยมจตุรัสใหญ่ที่มีค
ส่วนที่สองของหนังสือเล่มนี้เกี่ยวข้องกับการคำนวณหาพื้นที่และปริมาตรของรูปทรงเรขาคณิต ภาคตัดกรวยและปิระมิด ส่วนที่สามซึ่งมีเนื้อหามากที่สุดเกี่ยวข้องกับการประยุกต์ใช้เพื่อแก้โจทย์ปัญหาเกี่ยวกับมรดก
อัลคอวาริซมีย์ได้รับการสนับสนุนจากเคาะลีฟะห์อัลมะมูนในการเขียนตำราเล่มนี้ เพื่อใช้แก้โจทย์ปัญหาต่างๆที่เกี่ยวกับการแบ่งมรดกตามกฏหมายอิสลาม การค้า รังวัดที่ดิน การหาพื้นที่และปริมาตร การออกแบบ ขุดลอกคูคลองและการก่อสร้าง ฯลฯ ที่เกี่ยวข้องกับชีวิตประจำวัน ทำให้นักวิชาการมุสลิมยุคต่อๆมาสามารถคำนวณค่าของมุมและความยาวของด้านทั้งสามของสามเหลี่ยมและสามารถศึกษาวิชาดาราศาสตร์ได้ลึกซึ้งยิ่งขึ้น อัลคอวาริซมีย์ยังได้พัฒนาเทคนิคการคูณแบบแลทลิซ(Lattice Multiplication Method) เทคนิควิธีนี้ถูกนำเสนอต่อมาในยุโรปโดยฟิโบนัคซี
หนังสือ al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wal-muqābala ถูกแปลเป็นภาษาละตินโดยโรเบิร์ต เชสเตอร์ ในปี ค.ศ. 1145 ในชื่อ Liber algebrae et almucabala เป็นที่มาของคำว่า Algebra (พีชคณิต) ในภาษาอังกฤษ และถูกใช้สอนในมหาวิทยาลัยต่างๆของยุโรปยุคกลาง จนถึงคริสตวรรษที่ 15
ผลงานทางคณิตศาสตร์อีกเล่มของท่าน คือ Kitāb al-Jam‘ wat-Tafrīq bi-Ḥisāb al-Hind (ตำราว่าด้วยการบวกและลบตามการคำนวณของอินเดีย) ต้นฉบับภาษาอาหรับสูญหายไปแล้ว เหลือแต่ฉบับที่แปลเป็นภาษาละตินชื่อ Algoritmi de numero Indorum (al-Khwārizmī on the Hindu Art of Reckoning) ว่าด้วยการบวก ลบ คูณ หาร เลขฐานสิบและฐานหกสิบ การใช้เลขทศนิยม และการถอดรากที่สอง หนังสือเล่มนี้ทำให้เลขศูนย์และตัวเลขฮินดู-อราบิกแพร่หลายสู่ยุโรปและถูกใช้แทนตัวเลขแบบโรมันที่ยุ่งยากกว่า คำว่า algorithm ซึ่งหมายถึงลำดับของขั้นตอนการคำนวณที่ใช้แก้ปัญหาทางคณิตศาสตร์ก็มาจากชื่อของอัลคอวาริซมีย์นั่นเอง
ผลงานของอัลคอวาริซมีย์มีอิทธิพลต่องานเขียนของอุมัน อัลคอยยาม, ลีโอนาร์โด ฟิโบนัคซีแห่งเมืองปีซา (เสียชีวิตหลังปี ค.ศ. 1240) และมาสเตอร์ เจคอบแห่งฟลอเรนซ์ การอธิบายของอัลคอวาริซมีย์ปูทางไว้สำหรับการต่อยอดทั้งในเรื่องพีชคณิต เรขาคณิตและตรีโกณมิติ
อ้างอิงและอ่านเพิ่มเติม
- Philip K. Hitti, History of The Arabs : From the Earliest Times to the Present, Revised Tenth ed. New York: Palgrave Macmillan 2002
- Jonathan Lyons, The House of Wisdom : How the Arabs Transformed Western Civilization, Bloomsbury Press 2010.
- นิแวเต๊ะ หะยีวามิง, อัลฟาลัก ดาราศาสตร์ปฏิบัติสำหรับมุสลิม สำนักพิมพ์อิสลามิก อะเคเดมี
- Dr W.Hazmy C.H. Biography Muslim Scholars and Scientists,Islamic Medical Association of Malaysia
- N. Akmal Ayyubi, Contribution of Al-Khwarizmi to Mathematics and Geography http://www.muslimheritage.com/.../contribution-al...
- Joseph A. Kéchichian,The father of algebra: Abu Jaafar Mohammad Ibn Mousa Al Khwarizmi http://gulfnews.com/.../the-father-of-algebra-abu-jaafar...
- Jeff Oaks, Was al-Khwarizmi an applied algebraist ? http://pages.uindy.edu/~oaks/MHMC.htm
-------------------------------------------------------------
เรื่องที่เกี่ยวข้อง
